A while ago one of my aunts posted that 3 of her Facebook friends were having a birthday that day. It seems like a remarkable coincidence, but is it? This observation is reminiscent of a well known problem in probability that yields a surprising result.
The Conventional 2 Birthday Problem
The conventional probability theory known as the birthday problem or birthday paradox concerns the probability that, given a group of N people, at least two such people in the group have the same birthday. As it turns out, the probability is probably higher than you think.
What makes this problem non-intuitive is that we are not measuring whether you have the same birthday as someone else but whether any two people have the same birthday. So we don’t care so much about how many people are in the group but how many pairs of people are in the group, and that number grows much faster. In a cozy group of 5 people there are only 10 pairs, but in a classroom of 25 students there are 300 pairs.
OK, back to the question: How likely is it that a pair of people in a group have the same birthday? It should be the probability that two people have the same birthday (about 1/365, assuming all birthdays are equally likely and ignoring leap days) times the number of pairs in that group, right? Well, no. It’s not that easy. (Nothing in stupid probability ever is.) You also have to take into account the possibility that more than one pair has the same birthday, and that’s where things get complicated.
I use a trick to solve this problem. Rather than compute the probability that two people have the same birthday, compute the probability that no one has the same birthday as anyone else. To compute that, I consider the people one at a time (in an arbitrary but fixed order). The first person has no one to pair with, so the probability of no same birthday is 1 (100%). The second person will not match with the first person with probability 364/365. The third person will not match with the first two with probability 363/356. And so on. Just multiply those numbers up and take the inverse. There is your solution.
$$ \mathrm{P}(\textrm{shared b-day for } N) = 1 - \frac{356 \cdot 364 \cdot 363 \cdot 362 \cdots (366 - N)}{365^{N}} $$
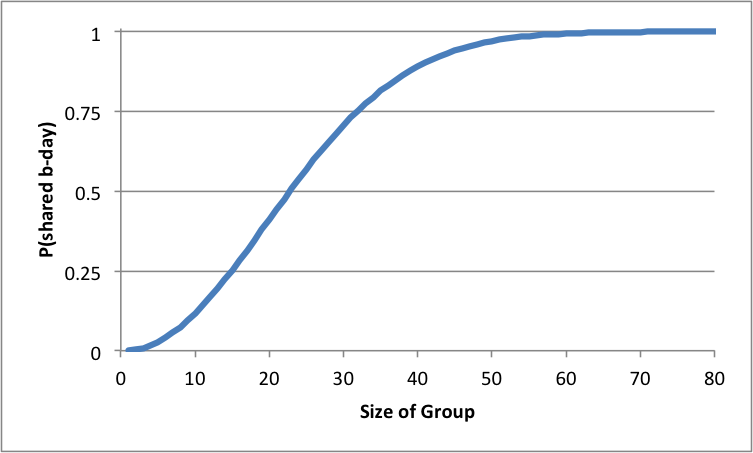
The plot at right shows the probability that at least one pair in a group has the same birthday for increasing group sizes. Surprisingly with a group of people as small as 23, it is even money whether some pair will have the same birthday. At a group of size 57, there is a 99% chance for a birthday collision! My probability teacher once suggested that this is an amusing property to try out at parties. (Of course, I’m guessing that means my math teacher wasn’t invited to many parties.)
The 3 Birthday Problem
Interesting (or, at least, I find it interesting), but so far we haven’t addressed my aunt’s situation where 3 people have the same birthday. The conventional birthday problem tells us nothing about the 3 birthday problem although it leads me to suspect the probability is greater than what intuition would tell you.
So what is the probability for, given a group of people, that three have the same birthday? The answer is… I don’t know. The trick I used for a pair of people doesn’t work for 3, and the counting just gets too complicated for my little brain.
Fortunately, I have another trick up my sleeve. Rather than figure out the exact solution, I can write a simulator program to estimate the probability. Here’s how it works. The simulator sets up an empty (virtual) room. It then lets in people one at a time. Each person coming in has a random birthday. The simulation continues doing this until someone comes in with a birthday that completes a triple.
That, of course, does not give us any probabilities. If we run the simulation again, we will (probably) get a different answer. But, if we run the simulation enough times, we can estimate the probabilities as the percentage of times the simulated group had 3 people with the same birthday. There is a very rigorous branch of computational science to determine the number of samples needed and the uncertainty remaining. But screw all that; I just ran the simulation for an excessive 100,000 times. For those who would like to run the simulator yourself, I have the code posted here.
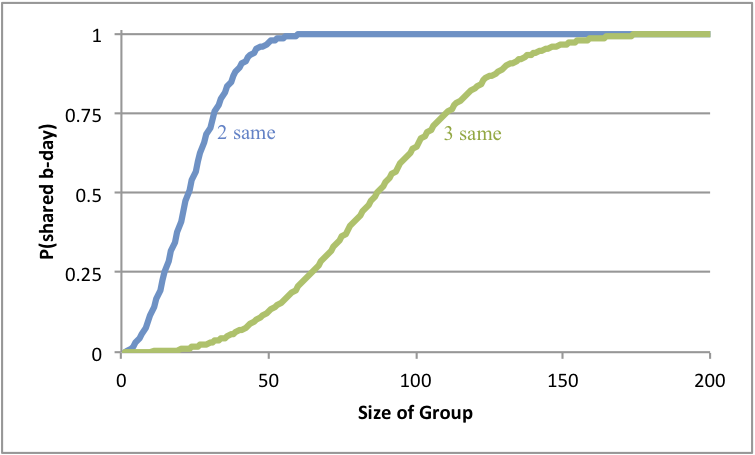
The plot at right shows the probability that at least one set of three people in a group has the same birthday for increasing group sizes. (The plot for groups of size 2 is also shown.) We see that the 3 birthday problem does indeed behave very similarly to the 2 birthday problem, but with expected shifted probabilities. With only 87 people in the group, the probability of having 3 simultaneous birthdays is 50%. Having 87 “friends” is pretty common for even casual Facebook users. Heck, I have more than 100 friends despite being unpopular and generally annoying. I see that my aunt now has about 150 Facebook friends. That makes having 3 friends with the same birthday pretty darn likely at over 96% probability.
Even More Coincident Birthdays
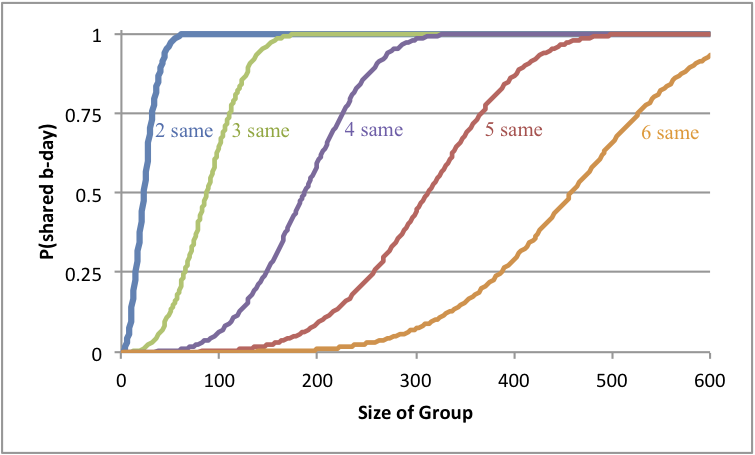
But why stop there? How likely is it to have 4 birthdays the same? Or 5? Or 6? The nice thing about using the simulator is that it is easy to expand to larger counts (you just have to wait longer). If you took a look at my simulator code, you may have already noticed that it measures up to 6 simultaneous birthdays.
Here is a report of how likely it is to have up to six simultaneous birthdays. (The full data for this plot are posted here.) As we increase the number of simultaneous birthdays, we need a larger group size to make it probable. (No surprise there.) Also note that the behaviors of these curves are similar. They all start off unlikely and then the curve dramatically bends upward.
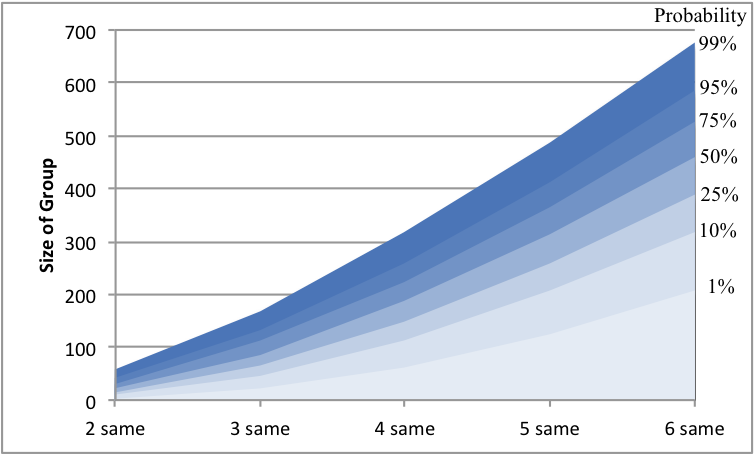
This next plot demonstrates the trend of the N birthday problem. The plot shows the size of the group necessary to hit a particular probability for each version of the birthday problem. At the top of the filled lines is the group size for a 99% probability, which I take for almost certainty.
What I find most interesting about this plot is the grouping of the middle quartiles, between 25% and 75%. Although this represents half of the probability space, these are bunched in a small group for every birthday problem. This is indicative of the sharp upward swing in the S shape of the curves.
Final Remarks
When I started speculating about the 3 birthday problem, I really had never considered anything more than the 2 birthday problem. I could not find any other references to the birthday problem with any more than pairs of identical birthdays although perhaps I just have bad Google-fu. It was gratifying to find that the solution matched my general expectation, which is so seldom the case in probability.
Anyone interested in probability or this problem should check out Wikipedia’s article on the birthday problem. It contains a much deeper analysis than I give here.
Finally, it is a little ungratifying that I was unable to come up with a closed solution for the 3 birthday problem. If you find one, let me know.